What was not clear in Agarwal's original paper was that this computational
short cut can be used in many cases other than the evaluation of (9).
If the derivation is carried out for the general case we discover that
the identity (30)-(33) holds whenever
is a symmetric function.
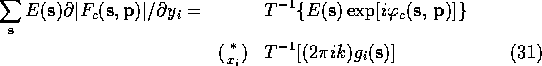
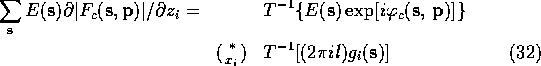
We can use (30)-(33) to speed up the calculation of the gradient of almost any function involving structure factors.
Let us develop an example. Suppose that we wish to minimize not the usual
function of the X-ray data (8), but the negative of the correlation
coefficient 
between the observed and calculated structure
factors, which can be cast as in (35), where the bar indicates
the mean value.
The gradient is given by
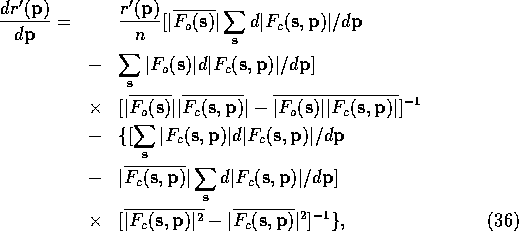
where n is the number of structure factors included. To calculate this gradient we need a number of means and three complicated summations, (37), (38) and (39):
From the generalized derivation we can see that these three quantities can be calculated from the same convolution, and, in fact, with the same program as the original calculation but substituting the three transformations given in (40)-(42):
Therefore with three FFT's we can calculate the required gradient of the correlation coefficient.
This particular function has not been implemented in TNT. To do so would only require the creation of the code to calculate the means, the coefficients for the transformations, and a program which would combine the means with the results of the convolutions to produce the final gradient. To perform refinement a program would have to be written to calculate r' for any given model. None of these programming tasks is difficult.
