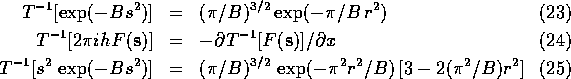To refine a structural model against crystallographic data both the function (8) and its gradient (9) must be evaluated.
Because the evaluation of the gradient involves a sum over all reflections for each parameter of the model, the calculation would be very time consuming if performed as in (9).
Agarwal (1978) showed that (9) can be expressed as follows:
where
This formulation requires a Fourier transform for each parameter and is also impractical. However, Agarwal separated the portion of (10)-(13) that depend on the atom (subscript i) from the rest of the factors and applied the convolution theorem to arrive at the following equations:
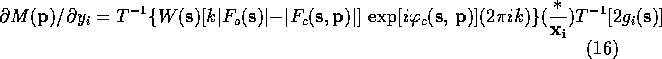
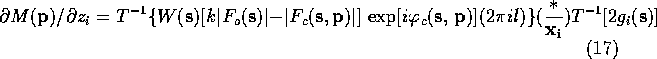
If the atomic scattering factor is modeled as a sum of Gaussians the second Fourier transform can be calculated analytically. For a given model, the first transform in each of (15)-(18) can be calculated with the FFT algorithm. In the form given in (15)-(18), it is necessary to perform three Fourier transform to determine the positional derivatives.
Lifchits (see Agarwal, Lifchitz & Dodson, 1981) has pointed out that the gradient can be calculate more efficiently by factoring (10)-(13) so that the first Fourier transform is the same in all the equations. The refactoring results in the following equations:
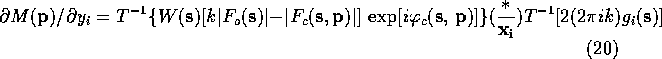
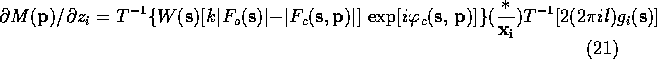
When these equations are used to calculate the gradient of 
,
only a single FFT is required. If one remembers that 
is
simply a sum of Gaussians, the Fourier transforms on the right can be
determined analytically by using the following rules:
