For planarity, 
is defined as the root mean square (r.m.s.)
deviation of the atoms from the best-fit plane.
Let N be the number of atoms in the plane and 
the
center of mass of the atoms. Consider
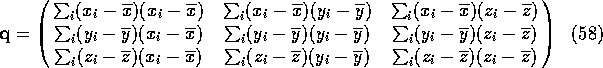
is the moments matrix for the atoms of the plane. The eigenvectors
of point along the directions of the principal axes of rotation of
this group of atoms. The eigenvalues of are inversely related to
the moments of inertia of rotation about the axis defined by the corresponding
eigenvector. The axis of rotation with the largest moment (smallest eigenvector)
is defined as the normal to the best plane for these atoms.
Let u be the smallest eigenvalue of , 
the eigenvector
of corresponding to u and 
( 
) be the
normalized eigenvector. Then the r.m.s. deviation of the atoms from planarity
is
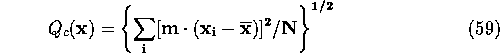
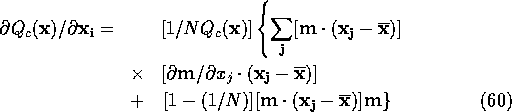
where 
is the outer product. It is defined, when 
and 
are column vectors, as 
.
The calculation of the derivative of the eigenvector with respect to the
position of an atom is difficult because eigenvectors are usually determined
algorithmically. There is no general equation which expresses the components
of the eigenvector of an matrix as a function of the components of that matrix.
However, if one assumes that the off-diagonal elements of are non-zero
one can derive an equation for the eigenvector:
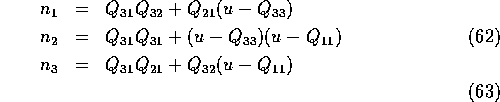
The derivatives of 
, 
and 
are simple to derive in terms of the
derivatives of the elements of . Because of the complexity of its
derivative we have made the assumption that the eigenvalue remains constant
during refinement.
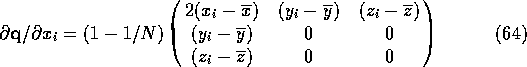
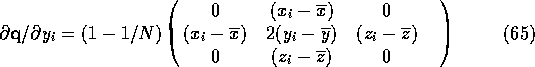
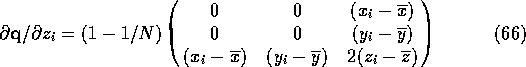
The assumption that the off-diagonal elements of are non-zero makes
the gradient calculation sensitive to the orientation of the plane. In the program
which performs these calculations the problems which might arise are ignored.
It is presumed that if by chance the plane lies in a special orientation the
movement resulting from the first cycle of refinement will cause it to be displaced
and subsequent refinement will function normally.