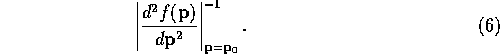
The aspect of the Full-Matrix minimization method which prevents it being used in common refinement is the difficulty in calculating the term
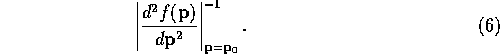
This matrix written out in full is
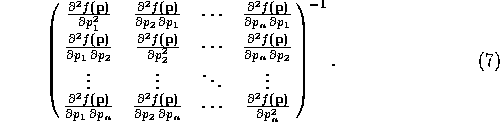
This matrix contains 
elements, where n is the number of
parameters in the model. In a typical case n will be on the order
of 10,000. The number of elements in the second derivative matrix,
often called the Normal matrix, would be 100,000,000. It would take
a lot of computer time to calculate it, a lot of memory to store it,
and a lot more computer time to invert it. The gradient descent
methods make various assumptions about the importance of different
parts of the Normal matrix to reduce these requirements.
To understand the relative importance of the different elements of the Normal matrix we need to understand the meanings of each part. The most important classification of the elements is the distinction between the elements on the diagonal and those off it. The elements on the diagonal are affected by a single parameter and are therefore somewhat easier to analyse. The off-diagonal elements are affected jointly by two parameters.
The information contained in the off-diagonal elements described how the effect on the function of changing parameter a is affected by changes in parameter b. In essence it is related to the correlation of the two parameters. If one considers the simple case where each parameter is varied in turn. Parameter a is moved to the value where the function in minimized. Then parameter b is changed. If the off-diagonal element for a and b is nonzero than parameter a will have to be readjusted, and the larger the value the greater the adjustment required.
The diagonal elements contain information about the affect of a parameter's value on its own affect on the function. This, of course, will always be large. (If the diagonal element is zero than any value for that parameter will be equivalent: a property which is usually undesirable in a parameter.)