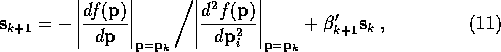
The Conjugate Gradient method is better than the Steepest Descent method because it uses some information about the normal matrix to improve the quality of the shift vector. It would seems reasonable to believe that the shift vector could be improved further if additional information were added. For instance, we can calculate the diagonal elements of the normal matrix directly, and quickly.
All this information is combined together in the Conjugate Direction method[5]. This method operates like the Conjugate Gradient method except it uses the shifts from the Diagonal Matrix method for its first cycle instead of the Steepest Descent method's. The shift vector in Conjugate Direction is
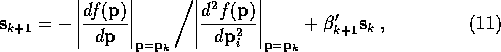
where the trick is calculating 
correctly. This matter
is discussed in detail in [5].