The conjugate gradient method uses the steepest descent method to produce its first shift direction, or ``seed" direction. The rate of convergence of early cycles can be improved if a seed that incorporates as much information as practical about the function is used. We would like a direction which will include compensation for the differences in the eigenvalues of the normal matrix. Because in X-ray crystallography the diagonal terms of the normal matrix dominate, a diagonal approximation to the normal matrix provides a powerful and quick alternative to the steepest descent method of generating shift directions. In this procedure the search direction is calculated by
where 
is the diagonal approximation to the normal matrix
for the parameters of cycle k. For the fastest rate of
convergence, this shift vector should be used as a seed for
conjugate
direction searches. It is not clear, however, how one
should calculate 
of Equation (6).
The refinement problems that we address are the wide range of magnitude of the eigenvalues of the normal matrix and the existence of off-diagonal terms. If we could choose a different set of parameters, for which the normal matrix was simpler, the rate of convergence would improve. Ideally one would choose a system of parameters such that all the eigenvalues were equal and all the off-diagonal elements were zero; then one cycle of steepest descent minimization would suffice.
Let us assume that we have determined a matrix ( 
) which will transform
the usual crystallographic parameters into such a set of parameters ( 
).
The transformations between the familiar parameters and the new ones will be
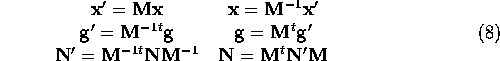
We can perform Fletcher-Reeves conjugate gradient minimization on the function using this new parameter space. The equations will be as before, Equations (4) thru (6), but with primes added:
Instead of working with the parameters we can substitute
back to the original 
parameters. The resulting equations are
In these equations the shift vectors, 
, are all premultiplied
by 
. It would be simpler to eliminate this complication
by simply defining 
. The
final equations for conjugate direction refinement, derived from recombined
parameters, but operating on the ``native" parameters are
At this point the matrix is undefined.
The optimal choice for would require that
,
the normal matrix for the new parameters, be equal to the identity matrix. To
calculate the optimal we need both the normal matrix and
its inverse; thus, we made no gains in computational
efficiency over the full matrix method.
However, if we recognize that in crystallography 
is
almost diagonal we can set 
.
Then 
in the Equations (15),
(16) and (17) will be replaced
by 
. Making this substitution we obtain
The seed direction ( 
when 
and
) is now the shift calculated from the diagonal
approximation to
the normal matrix, as we desired. In addition, however, we have an
equation for .
In summary, we have a minimization method where the diagonal terms of the normal matrix are explicitly included and the off-diagonal elements are dealt with via a set of conjugate directions.
Agarwal (1978) suggested a similar method; however,
his equation for was incorrect.
In the present nomenclature, his proposal for was
In conjugate gradient refinement is equal to ratio of the length of
the gradient at point k divided by that length at point k-1. Because k
should be closer to the minimum than point k-1, should be less
than unity.
An estimate of Agarwal's can be achieved by examining his for
cycle 2, which is
As before, the parameters after cycle 1 should be closer to the minimum than
the starting parameters, resulting in 
.
This value results in the undesirable outcome
that the previous cycle's direction is considered more important that the
direction
calculated from the current parameters. This now explains why Agarwal found
it necessary to place an empirical upper limit of 0.4 on .
The
value of calculated with Equation (19) typically falls
between 0.5 and 0.9. The empirical value of 0.4 falls closer to the typical
value than either setting to zero (and using the method of
Equation (7)) or using the equation of Agarwal(1978).
