The Steepest Descent method is very robust. It will smoothly converge to the local minimum whatever the starting parameters are. However it will require a great deal of time to do so. One would like a method which would reach the minimum quicker.
The problem with Steepest Descent is that no information about the normal matrix is used to calculate the shifts to the parameters. Where ever the assumptions break down (the parameters have correlation and have different diagonal elements) the shifts generated will be inefficient.
Just as one can calculate an estimate for the slope of a function by looking at the function value at two nearby points, one can estimate the curvature of a function by looking at the change in the function's gradient at two similar points. This experiment is routinely performed in Steepest Descent refinement. The gradient is calculated, the parameters shifted a little, and the gradient calculated again. In Steepest Descent the two gradients are never compared but if they were a bit of information about the normal matrix could be learned.
The Conjugate Gradient method[3] does just this. The analysis of Fletcher and Reeves showed that the Steepest Descent shift vector can be improved by adding a well defined fraction of the shift vector of the previous cycle. Each cycle essentially ``learns'' about one dimension of curvature in the n dimensional refinement space. Therefore after n cycles everything is known about the normal matrix and the minimum is found.
The shift vector for cycle k+1 using Conjugate Gradient is
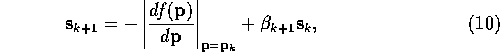
where 
is the ratio of the length of the function's present
gradient to its previous length. During the first cycle there is no
previous cycle. The first cycle must be Steepest Descent.
The fundamental limitation of the Conjugate Gradient method is that it is guaranteed to reach the minimum in n cycles only if the Taylor's series does indeed terminate, as assumed in equation 3. If there are higher order terms, and there are in crystallographic refinement, then n cycles will only get the model nearer to the minimum. One should start over with a new run of n cycles to get the model even closer.
Even n cycles is a lot in crystallography. No one runs thousands of cycles of Conjugate Gradient refinement, nor can they be run with current software. The shifts become too small to be represented with the precision of current computers. Small shifts are not necessary unimportant ones. These small shifts add up to significant changes in the model, but we cannot calculate them.