An analysis of the Full-Matrix method, and all gradient descent methods
begins with the Taylor's series expansion of the function being minimized.
For a generic function ( 
) the Taylor's expansion is
where 
is the current set of parameters of the model. In all cases
the additional terms (represented by `` 
'') are ignored. This
assumption has considerable consequences which will be discussed later.
We can change the nomenclature used in equation 2
to more closely
match those in refinement by defining to be the parameters of
the current model and 
to be a ``shift vector'' which we
want to add to . is equal to 
. The
new version of Equation 2 is
and its derivative is
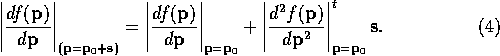
Since the first and second derivatives can be calculated given any
particular value for this equation allows the gradient of the
function to be calculated given any shift vector. In addition the
equation can be inverted to allow the shift vector to be calculated
given the gradient of the function.
At the minimum (or maximum) of a function all components of the gradient
are zero. Therefore we should be able to calculate the shift vector
between the current model ( ) and the minimum. The equation
for this is simple --
The Full-Matrix method is to use this equation, evaluated with the
current parameters, to calculate . is then
added to to give the set of parameters which cause the
function to be minimal, and in the case of refinement the best fit
to the observations.
This method sounds great. One calculates a single expression and the
minimum is discovered. When fitting a line to a set of points this
is exactly what is done. In refinement something is obviously different.
The difference arrises from the `` '' which we choose to ignore.
In the case of fitting a line to points the terms represented by `` ''
in fact are zero. The truncated Taylor's series is exact and the
shift vector is also exact. In refinement these terms are not equal to
zero resulting in the shift vector giving only the approximate location
of the minimum.
The quality of the estimate is limited by the size of
the terms which are ignored. The terms of the Taylor's series
have increasing powers of . The first term ignored is
multiplied by 
and the higher order terms are multiplied
by ever higher powers. If is small these higher order terms
become quite small also. Therefore the closer is to the minimum the
better estimate becomes.
The Full-Matrix method, and all the gradient descent methods which are
derived from it, becomes a series of successive approximations. An
initial guess for the parameters of the model ( ) is manufactured
somehow. For the shift vector to actually give an improved set of
parameters the guess must be sufficiently close to the minimum. The
``sufficiently close'' criteria is rather difficult to calculate
exactly.
The distance from the minimum at which a minimization method breakdown is called the ``radius of convergence''. It is clear is that the Full-Matrix method is much more restrictive than the gradient descent methods, and the gradient descent methods are more restrictive than simulated annealing, Metropolis, and Monte Carlo methods. Basically the less information about the function calculated at a particular point the larger the radius of convergence will be.
The property of the Full Matrix method which compensates for its restricted radius of convergence is its ``power of convergence''. If the starting model is within the radius of the Full Matrix method that method will be able to bring the model to the minimum quicker than any other method.
