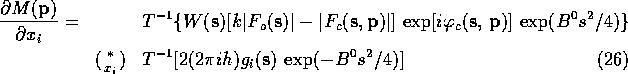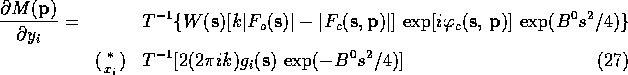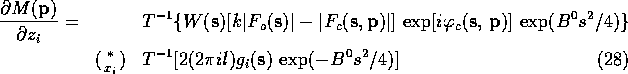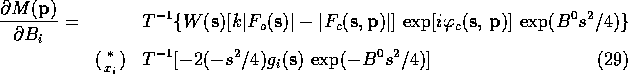The calculation of the convolutions in (19)-(22)
involves sampling each of
the functions at discrete points, multiplying the values point by point, and
summing all the products. The sampling interval required to represent a function with
a given accuracy depends on the magnitude of the high-resolution components of
that function. There is no problem determining the sampling interval for the
function on the left of the convolution because it contains no components of
resolution higher than the measured data. However, the function on the extreme
right-hand side of (19)-(22) are not of limited
resolution and therefore,
at least in principle, must be sampled on a very find grid. This problem existed
in the original equations (15)-(18) but is much more
serious with the new
form of (19)-(22) because the high-resolution
components are enhanced by
the inclusion of the crystallographic indices (h,k,l). This problem is most
severe in the calculation of the temperature-factor derivatives (22)
because of the 
factor. A mechanism to allow these functions to be calculated
using the somewhat coarser grid has been devised by recognizing that the errors
introduced by a coarse grid are fundamentally the same as those encountered in the
calculation of structure factors using the FFT method (Ten Eyck, 1977).
The solution involves `smearing' or `blurring' the function of interest so that
it is sampled by a larger number of grid points. The `smearing' must be
compensated elsewhere in the calculation. In this case the compensation is
achieved by `sharpening' the difference map. This can be done without introducing
additional errors because no new high-resolution terms are introduced into the
difference map. The final equations, as used in the program ADERIV, are
